Робот для состязаний: сортировщик - между корзиной и свалкой.

В предыдущих двух заметках (1, 2), было рассмотрено два аспекта решения задания для старшей группы из Международной робототехнической олимпиады. Первый аспект – определение стратегии по сколько кубиков робот будет захватывать и как он их будет перемещать. Второй аспект затрагивал некоторые особенности программирования робота для этого задания – как заранее предусмотреть возможность того, что корзины для сортировки могут располагаться в различных местах.

В этой заметке предлагается рассмотреть еще один аспект – как запрограммировать перемещение между свалкой и корзинами.

Направление наших рассуждений будет строится от одной из главных характеристик робота – сколько объектов за раз он может перемещать. Можно выделить два основных случая: перемещение за раз только одного кубика, перемещение за раз нескольких кубиков.

Сначала рассмотрим первый случай - перемещение только одного кубика за раз.

В прошлый раз обсуждалось две возможности перемещения по одному кубику: 

1. Выбираем кубики по одному сначала с одной стороны свалки и сортируем их, затем тоже самое делаем с кубиками с другой стороны свалки.
   
   Очевидно, что в этом случае нам нужно счетчик, который бы считал, сколько кубиков с какой стороны свалки осталось. Как только кубики с одной стороны закончились, то ехать к этой свалке не имеет смысла, начинаем двигаться сразу к противоположной.
   
   Но как роботу переместиться от свалки к корзине и обратно?
   
   Вообще, возможно несколько вариантов перемещения:
   
   1. Когда любое перемещение проходит по срединной черной линии.
      
   Этот способ хорош тем, что при нем, черные полосы могут служить ориентирами для передвижения робота. Самое простое – робот всегда использует черную линию – двигается по карте вдоль нее. А уж если в программе робота, при его передвижении, ведется учет количества пересеченных черных линий, то такой робот сможет всегда сказать в какой области карты он сейчас находится.
   Для перемещения робота, в данном случае, на срединной черной линии выбирают опроную точку – место на карте, от которого строятся пути-маршруты во все возможные места назначения. Таким образом, робот всегда будет знать, от какой точки ему нужно всегда отправляться к той или иной корзине.
   Движение робота при этом методе можно описать следующим образом:
   Если рассмотреть несколько вариантов опорных точек, то неплохой опорной точкой является место посредине между свалками. В таком случае, в программе должны быть предусмотрены следующие маршруты:
   
   • из опорной точки в корзину 1
   • из опорной точки в корзину 2
   • . . .
   • из опорной точнки в корзину 7
   • из опорной точнки в корзину 8
   • из опорной точки к левой свалке
   • из опорной точнки к правой свалке
   • путь от корзин с левой стороны к финишу
   • путь от корзин с правой стороны к финишу
   Каждый такой маршрут удобно представить в виде отдельной процедуры (My Block).
   Маршрут может просто состоять из трех движений, расчитанных по определенному расстоянию. А может быть и в виде более сложного (но более универсального) алгоритма, учитывающего количество пройденных пересечений с черными линиями.
   Но если дистанцироваться от его реализации и применить код для определения нужной корзины, подобный тому, что описывался в предыдущей заметке. То структура программы будет выглядеть следующим образом:
   При использовании блоков возникает еше положительный организационный момент – каждый блок может писаться и тестироваться отдельным человеком. Действия, необходимые выполнить в блоках – очень простые, их смогут написать даже новички в Lego-программировании. Т.е. даже при небольшой команде – преимущество на лицо – как команда, они напишут все блоки быстрее.
   
   2. Перемещение проходит сразу вдоль корзин (как вариант вдоль боковых черных линии).
      
      Этот метод даст выигрыш в скорости выполнения задания, по сравнению с предыдущим, поскольку для корзин, расположенных с той же стороны, что и соответствующий кубик на свалке, робот не будет тратить время на выезд к срединной линии, а сразу направится к корзине. До корзин, находящихся на противоположной стороне, траектория движения не регламентируется этим методом. Например, она может быть тоже с перемещением по срединной линии.
      Описать работу робота, функционирующего по данной схеме, можно следующим образом:
      
      Следует заметить, что несмотря на упрощенную общую схему метода, части программы, отвечающие за перемещение робота к корзине и, наоборот, к свалке, напротив, усложняются. Это связано с тем, что в предыдущем методе, робот двигался к корзинам всегда из одного места на карте – опорной точки. В этом же методе такого места нет, и робот должен знать, как минимум, два способа добраться до каждой корзины – один способ - с левой свалки, другой – с правой. Соответственно, увеличиться и количество способ перемещения от корзин к свалкам – от каждой корзины нужно уметь попадать как к левой свалке, так и к правой.
      
   3. И самый сложный, прямолинейный.
      
      Этот способ имеет опять же преимущество в выборе оптимальной траектории перемещения робота от свалки к корзине и наоборот, по сравнению с двумя предыдущими. Если во втором способе опимизировалась только траектория перемещения к корзинам, находящимся на той же стороне, что и свалка. То данный способ оптимизирует также траекторию движения до корзин на противоположной стороне.
      С точки зрения основной структуры программы, этот способ ничем не отличается от предыдущего. Для него также харакерны два разных пути достижения одной и той же корзины, но из разных свалок. Существенная разница будет в реализации метода достижения корзины, располагающейся на противоположной стороне от свалки. Тут можно использовать, как сложный метод, подобный тому, что описан здесь. А можно и более простой, но менее надежный.
      
2. Алгоритмы рассмотренные выше оперируют вначале кубиками только с одной стороны. Другой подход – ехать за новым кубиком к той свалке, которая находится на той же стороне, где и последний выгруженный кубик.
   
   Поскольку в этот метод подразумевает, что движение к свалке будет происходить по оптимизированной траектории (напрямую к свалке), то способ возврата к свалке с использованием опорной точки особого смысла здесь не имеет. Остальные два способа, описанные ваше, выглядят вполне подходящими, единственное, что будет отличать конечные реализации для данного метода – алгоритм выбора следующей свалки.
   Раньше он был простым – если количество обработанных кубиков стало меньше 5, то свалка должна "рабочая" свалка теперь будет другая.
   
   Сейчас, алгоритм выбора значительно усложниться за счет того, что надо хранить информацию с какой свалки сколько кубиков обработано. Эта информация будет помогать определять те случаи, когда робот должен будет ехать на "неоптимальную" свалку, после того, как все кубики из "оптимальной" свалки выбраны.
   

Для более сложных конструкций, когда робот способен забрать из свалки больше, чем один кубик, также доступны три разных способа прокладывания маршрута: через срединную линию, вдоль корзин, прямолинейное. Только теперь, после выгрузки кубика в корзину, робот не всегда возвращается к свалке. Вместо этого, он может сразу же двигаться к следующей корзине.

В этом свете, проще всего выглядит реализация алгоритма движения вдоль срединной линии. В ней опять же используется опорная точка, выбранная достаточно оптимально для достижения любой из возможных корзин. Все маршруты тогда строятся относительно этой точки.

Рассмотренный ранее подход с использованием опорной точки, для сортировки роботом, способным за раз перемещать два и больше кубиков, не оптимален. Это видно, даже из представленного выше расположения сортировочных корзин и кубиков. Так, например, чтобы отсортировать первые два кубика из левой свалки, роботу нужно будет проделать следующий маршрут.

Да, конечно, можно поиграться с расположением опорной точки, и это даже может принести положительные результаты для какого-нибудь «удобного» расположения кубиков и сортировочных областей. Но просто ожидать такой удачи, довольно безрассудно, поэтому логично выглядит попытка придумать какой-нибудь универсальный алгоритм.

Например, что если ехать сразу к интересующей робота корзине, минуя опорную точку.

Поскольку кубики могут быть расположены произвольно, то нельзя заранее сказать из какой корзины в какую нужно будет перемещаться роботу. Тогда в реализации такого подхода, необходимо предусмотреть возможность перемещений в любую корзину из любой.

"Ага!", воскликнут те, кто дружит с математикой – "у нас 8 потенциально возможных мест куда нужно будет вести первый кубик, и 8 мест куда нужно везти второй кубик. Т.е. из каждой корзины, нужно проложить 8 различных маршрутов, и таких корзин - 8. Итого, это 8x8=64 различных комбинаций корзин, 64 различных маршрута!"

Да, но нужно посмотреть что из себя представляют эти маршруты.

1. Перемещаемся в соседнюю правую корзину
   1-2, 2-3, 3-4, 5-6, 6-7, 7-8
   
2. Перемещаемся в соседнюю левую корзину
   2-1, 3-2, 4-3, 6-5, 7-6, 8-7
   
3. Перемещаемся в право через одну
   3-1, 4-2, 5-7, 6-8
   
4. Перемещаемся влево через одну
   1-3, 2-4, 7-5, 8-6
   
5. Перемещаемся вправо из крайней корзины в крайнюю
   5-8, 4-1
   
6. Перемещаемся влево из крайней корзины в крайнюю
   1-4, 8-5
   
7. Перемещаемся в противоположную корзину
   1-5, 5-1, 2-6, 6-2, 3-7, 7-3, 4-8, 8-4
   
8. Перемещаемся со сдвигом на одну корзину вправо
   2-5, 5-2, 3-6, 6-3, 4-7, 7-4
   
9. Перемещаемся со сдвигом на одну корзину влево
   1-6, 6-1, 2-7, 7-2, 3-8, 8-3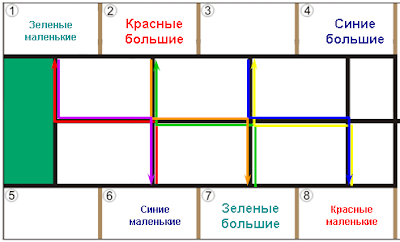
   
10. Перемещаемся со сдвигом на две корзины вправо
    3-5, 5-3, 4-6, 6-4
    
11. Перемещаемся со сдвигом на две корзины влево
    1-7, 7-1, 2-8, 8-2
    
12. Перемещаемся из крайней левой корзины в крайнюю правую на противоположной стороне
    4-5, 5-4
    
13. Перемещаемся из крайней правой корзины в крайнюю левую на противоположной стороне
    1-8, 8-1
    

Проверим, все ли переходы покрыты:

Где, "Z" – роботу никуда двигаться не надо – просто положить следующий кубик в ту же самую корзину.

Все. Таким образом, видно, что нужно запрограммировать всего лишь 13 различных перемещений робота, для того чтобы обеспечить его передвижение между любой парой корзин. 

Проверка того, все ли перемещения покрыты спецаильно сделана в виде матрицы – именно таким образом можно задать в программе, как роботу двигаться после того как он положит кубик в нужную корзину.

Самый простой способ реализовать эту матрицу на NXT-G, если закодировать каждую ячейку матрицы числом:

Т.е. для описания такого массива в программе нам нужен будет блок Switch с 64-мя вкладками.

Также необходимо будет релизовать 13 подпрограмм (MyBlock) ответственных за то или иное перемещение. 

Как только все 13 подпрограмм готовы, их нужно будет разместить аккуратно в нужных вкладках. Например, Блок "А" во второй, одиннадцатой, двадцатой и т.д., а блок "M" в восьмой и пятьдесят седьмой вкладках.

Тогда к этим подпрограммам можно обратиться с помощью следующего кода: